Courses/Computer Science/CPSC 203/CPSC 203 Template/Lecture Template/Lecture 8
Contents
Housekeeping
(none)
Required Reading
fluency textbook: Chapter 16: A Table with a View pp 442- -- 445 , 453--478
Recap of Concepts from Lectures 1 - 7
In these first set of lectures, we have created a "frame" for problem solving by introducing a critical series of key concepts that apply to any problem solving situation, and specific concepts that illustrate problems, and conceptual tools that help us to solve specific problems.
The Problem Solving Frame
We've introduced the following sets of terms, that reflect specific aspects of problem solving. With each of these terms:
- Attempt a capsule definition (then check it against your previous notes).
- Compare and Contrast each of the terms on a single line (e.g. like algorithm and heuristic).
- Give a specific example or instance of each term.
Terms
- Algorithm and Heuristic (Lec. 1) -- two specific entry points to problem solving.
- Working Hypothesis and Error (Lec. 2) -- a pair of terms which allow us to compare our expectations against our observations.
- System, Design, Evolution (Lec. 3) -- a triplet of terms that are common in any discussion of a complex, multi-faceted problems, whether in the technical, biological, or social realms.
- Model (Lec. 4)-- a representation of our understanding. We've emphasized the building of simple "Dots and Edges" models, based on graph theory.
- Information System, Information Hierarchy (Lec. 5) -- the system and process by which data is brought to people as information, and eventually knowledge.
Concepts and Tools
- Internet's Structure and Design (Lec. 2-3). Original design as a highly connected network, and subsequent evolution to a scale free network (Lec 2-3). Introduces the problem, "What does the Internet Look Like", and uses it as a way of discussing the current capabilities and limitations of the Internet, and examining alternate designs for a future Internet.
- Graph Theory (Lec. 4). Basic terms and concepts in graph theory that help us build and analyze models.
- Spreadsheet Data Model (Lec 5). Simple graph model of spreadsheet that emphasizes it's central nature as carrying values from cell to cell via functions. This flexibility allows it to serve in many cases as an idea sketchpad.
- Visual Introduction to Data Analysis (Lec 6-7). Key data analysis concepts, emphasizing
- visual understanding of data analysis within a grid-like space (that could be represented via a spreadsheet)
- small set of visual design concepts and graphic perception paradigm that allow us to effectively represent data as pictures, via charts.
Polya's Suggestions
We will delve into Polya's suggestions for problem solving later in the course For now, we have covered the broad outlines of his suggestions. You might find these suggestions particularly useful when working on Assignment 1, Assignment 2, your Term Projects.
- First, Understand The Problem
- What is Known, Unknown
- Draw a Figure
- Second, Devise a plan.
- Find the connection between the data and the unknown (i.e. what is missing).
- Have you seen this problem before? Is there a related problem you know how to solve?
- Third, Carry out the plan.
- Check each step. Is it correct? Can you "prove" it is correct?
- Fourth, Review/Extend the plan.
- Is this the best solution?
- Could you solve this differently? More simply?
Introduction
Relational databases are nominally ways of storing masses of data. They are also, from the problem solving perspective, ways of asking questions when data is available. It is this aspect of relational databases that we will emphasize through the next several lectures.
Today we introduce some basic concepts in set theory needed to understand the basics of Relational Databases, and introduce the core model for a relational database.
At the end of today's lecture you will have:
- been introduced to basic concepts in Set Theory
- practices simple examples of problem solving using Sets
- be introduced to the core model for relational databases, as a graph connecting various sets of information about data: domains, entities, attributes, relations.
Just as Graph Theory gave us some basic tools we can use to build models of various complexity, set theory will give us some basic tools for understanding databases as a problem solving medium based on asking questions about data. The style of problem solving based on set theory (and by extension relational databases) requires practice to master, and practicing this style of thought will be emphasized in the next several lectures.
Glossary
- Venn Diagrams -- a visual method of representing sets invented by the Reverend John Venn. A square box represents the "Universe" of discourse, and circles within that box represent sets, and the different kinds of operations one can do on sets. On the overheads we will introduce Venn diagrams for each Set Concept, and the associated mathematical notation. For more on Venn digarms, see: [Venn diagrams]
- Set - A set is a collection of unique objects. In databases, all information si represented by sets and subsets. Sets, Subsets, Supersets, Intersection sets and Union sets are introduced in class via "Venn Diagrams".
- Elements -- individual items that are members of a set. For example, "Fido" might be a member of the set DOGS.
- Null Set -- and imaginary set with no elements.
- Intersection Set -- Given two sets, A and B, the intersection set is the set of those objects that exist BOTH in SetA AND SetB
- Union Set -- Given two sets, A and B, the union set is the set of those objects that exist in EITHER SetA or SetB.
- Set Complement -- All the items NOT IN a set A.
- Set Difference -- Given two sets, S and T, the difference S - T (also denoted S/T) is all the items that are elements of S and that are not elements of T.
- Disjoint Sets -- If two sets, S and T, have no elements in common, they are called disjoint sets.
- Subset -- Set B is a subset of A, IF all members of B are also in A.
- Superset -- Set A is a superset of B, if all members of B are also in A.
- Cartesian Product of Sets -- Given two sets, S and T, the cartesian product pairs every element in S with every element in T. If we label an element in S as s, and an element in T as T, the cartesian product is the set of all ordered pairs (s,t).
- Cardinality of a Set -- The number of elements in a set.
- Powerset -- the set of all subsets of a set. If S is the cardinality of a set, the cardinality of the powerset is 2**S
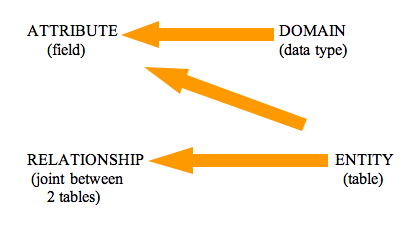
- Domain – “Data Type” = accepted values and operations. A set of values of a specific type with allowable operations that can apply to many attributes. Every field or column must be assigned a data type which is a domain (with specific rules) such as:
- Text
- Numeric
- Integer
- Date
- Hyperlink
- Attribute – a feature of an entity (a "variable")
- Entity – an object in the world, which can have many relationships with other entities
- Relationship – A link between two entities. If the entities are objects in the world, the relationship between them could be considered a verb.
- Table - A row (case) by column (variable) display. An entity that has a group of related records. In Relational Databases, a table if often called a "Relation". It is also called an "Entity". Each variable is of a particular data type (domain)
Many of the set theoretic concepts we introduce today were first developed by Georg Cantor, a uniquely creative mathematician.
For more on Cantor, see: [George Cantor]
At its induction, Set Theory was highly controversial, because of the "contradictions" it introduced, such as Russel's Paradox, which loosely stated is, "What is the Set containing Sets that are not members of themselves". For more on Russel's Paradox see: [Russel's Paradox] Cantor's development of a concept of infinite sets via the notion of Power Sets also created some lasting controversies [Cantor Controversy]
Controversial or not, set theory is a basic component of modern mathematics, and the foundation of relational database theory.
Concepts
In this lecture we will move through the following concepts:
- A basic concept of sets, illustrated as Venn diagrams, and introducing the traditional mathematical notation.
- Solving simple problems using Venn Diagrams.
- How data can be represented as sets
- The Core Relational Database Model
Relational DB Meta Model
This model is also called the Relational Database Meta Model, as any specific model in a relational database corresponds to an instance of it.
Summary
(to be added)
Text Readings
See Required Readings above.
Resources
Many of the Set Definitons, and several sample problems were modified from the following two texts:
Wallis, W.D. 2003. A Beginner's Guide to Discrete Mathematics. Birkhauser.
Greg, J.R. 1998. Ones and Zeroes. Understanding Boolean Algebra, Digital Circuits, and the Logic of Sets. IEEE Press.
Homework
Use Venn diagrams to illustrate the following situations.
- Fire engines are red, but not round. Baseball's are round, but not red. Apple's are round and red. Draw a Venn Diagram of two sets, Red, and Round. Locate in this diagram: Fire Engines, Apples, Baseballs.
- All big Canadian cities are near large lakes. Calgary is not near a large lake. Therefore Calgary is not a big Canadian city.
- All bankers are wealthy. All students are cheerful. Bill is a banker. No cheerful people are wealthy. Therefore Bill is not a student.
- All programmers are solitary people. All communications students are social. No solitary people are social.
- All designer clothes are expensive. None of my clothes are expensive. All expensive clothes are well made.