Courses/Computer Science/CPSC 203/CPSC 203 Template/Lecture Template/Lecture 19

Introduction

In this lecture we will introduce a Functional Approach to Problem Solving, once again using Boolean Logic as our example. A Functional Approach to Problem Solving is a natural process to move from Algorithm (a mechanical procedure) to Program (an implementation of an algorithm). We will illustrate this approach by building small functional programs to represent the basic Boolean operators and circuits we have learned.

At the end of this lecture you will:

• Be introduced to the idea of beginning a program with a description of an algorithm
• Be introduced to the "functional programming" style, in which one begins with simple functions, and then builds more complex functions from them.
• Be able to view each of the Boolean operators as simple functions that can be combined to make more complex functions.

Concepts

While we introduce these concepts of Pseudocode Driven Programming and the Functional Style of Programming in the context of Boolean Logic and Circuits we have studied -- these approaches can be used to develop any program. And, even when one is not programming, they provide a natural design technique for breaking a problem down into small pieces, and building a solution up from those pieces.

Pseudocode Driven Programming

This is a simple approach to programming which allows one to move from a natural language description of an algorithm to a more formal description in some programming language.

1. State the algorithm in plain English.
2. Write out each major step in the algorithm as a comment
3. Fill in the code that matches the comment
4. If there are more than a few lines of code required
   1. Break the comments down further

The result of this style of programming is that

1. You must think through your algorithm before codeing
2. The resulting code is well commented and easy to read
3. For those reasons, it is easy to debug.

Functional Style of Programming

The functional style of programming is very similar to the idea we learned in databases of building an analysis up out of sequential queries, where the output of one query is input to the next. In this case, you begin with building simple functions; and then more complex functions that call those simple functions.

The basics of the Functional Style of Programming could be summarized as follows:

1. A function should do ONE THING ONLY. The one thing it does is Return a Value. That Value can then be used as input to another function.
2. Identify the simplest functions you can build.
3. Build these functions first.
4. Build more complex functions out of the simpler functions.
5. If a function appears to be doing more than one thing only, break it down into 2 (or more) functions.
6. If you can't build the function you want out of existing functions -- identify the next function you need to build.
7. If a function looks to be getting quite long -- think whether you could break it down into simpler functions.
8. If the same pattern of code shows up in several functions -- can you put this pattern into it's own function.

The result of this style of programming is that:

1. Functions are re-usable in several programs
2. You can effectively treat a well detailed and error-checked function as a black box, or "lego" piece that can be used to construct larger functions.
3. Large programs, are essentially constructed out of many small functions --each of which is relatively easy to understand.
4. You usually need to debug within a particular function --- and not everywhere through a large program.

Examples using Boolean Logic

==== Brief Review ==== (from lecture 17)

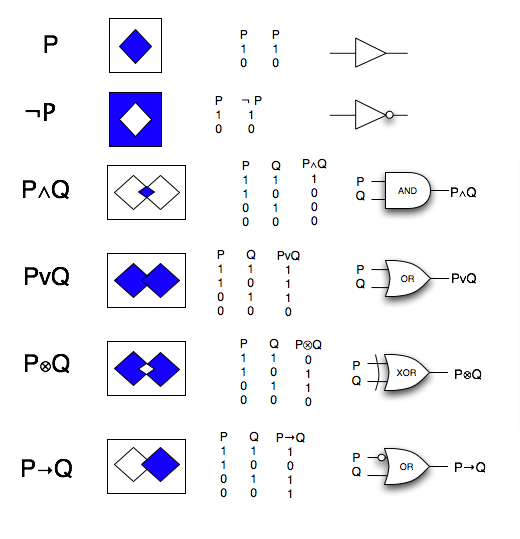
This is a summary of the basic Boolean Logic operators we have covered so far, from three different view points:

• Set Theoretic Interpretation
• Truth Table Representation
• Circuit Diagram Visualization of a Truth Table.

3 Views : Set Theory, Truth Tables & Circuits

Note: for P--> Q, the rectangle that surrounds the squares should be fully shaded.

Code Examples

Below are examples of the simple Boolean Functions we built in class today, with some error simple error checking code added. Note: the lines in bold are actually marked by triple quotation marks before and after (a form of commenting in Python).

---

Boolean Functions

  def booleanIdentity(x1):
      booleanIdentity Rule: Return x1 
      # Check that input is a boolean value
      checkBooleanInputs(x1,0)
      return x1

  def booleanNot(x1):
       booleanNot Rule: Return the absolute value of 1 -x1
       # Check input is a boolean value
       checkBooleanInputs(x1,0)
       return abs(1-x1)    

  def booleanAnd(x1,x2):
       booleanAnd Rule: An AND function takes the minimum of its inputs
      # Check the Inputs are Boolean values 0/1
      checkBooleanInputs(x1,x2)
      # Apply AND Rule
      return min(x1,x2)

  def booleanOr(x1, x2):
       booleanOr Rule: An OR function takes the maximum of its inputs
      #Check the Inputs are Boolean values 0/1
      checkBooleanInputs(x1,x2)
      #Apply OR Rule
      return max(x1,x2)

  def booleanXor(x1,x2):
   boolean Xor Rule: If AND=1, Return 0; else Return OR
   #Check the Inputs are Boolean values 0/1
   checkBooleanInputs(x1,x2)
   # AND=1, returns 0
   if booleanAnd(x1,x2) ==1:
       return 0
   # else return OR
   else:
       return booleanOr(x1,x2)

  def booleanImplication(x1,x2):
       booleanImplication Rule: Not-X or Y
      # Check Inputs are Boolean values 0/1
      checkBooleanInputs(x1,x2)
      # Not X
      notX = booleanNot(x1)
      # Or Y
      boolImp = booleanOr(notX,x2)
      return boolImp

  class BooleanError(Exception):
      def __init__(self, msg, x1, x2):
          self.arg = (msg, x1, x2)
          self.msg = msg
          self.x1 = x1
          self.x2 =x2
      def __str__(self):
          return str(self.arg)

  def checkBooleanInputs(x1,x2):
      Raises an Error Message if Inputs are not 1 or 0
      if (x1 not in [1,0]) or (x2 not in [1,0]):
          raise BooleanError ("NonBoolean Inputs", x1, x2)

Summary

• You were introduced to two complementary styles of Programming: Pseudocode driven programming and the Functional Style of Programming.
• The basic Boolean operators and circuits you have previously been introduced to are now represented as small programs that implement both the Pseudocode and Functional styles described in this lecture.

Homework

1. As we did in class, build some simple circuits, and trace the result that the matching program would produce.
2. Extra Practice: If you have downloaded Jes or Python at home -- try building some simple functional style programs -- based on simple algorithms. A good example might be, building up some basic statistics: e.g. the mean, standard deviation, mode, median.

Questions

• /Lecture 19 Questions