Courses/Computer Science/CPSC 203/CPSC 203 Template/Labs Template/Advanced Examples for Programming
Contents
Advanced Examples for Programming
Instructors and TAs please upload your examples . Also provide the following information:
- Topic or Concept you are illustrating
- Your name
- Brief written (or graphic) illustration of concept, and example code.
Functional Style of Programming --Mishtu Banerjee
(This Material from Lecture 19, Fall 08 Section L04; lecture notes at:http://wiki.ucalgary.ca/page/Courses/Computer_Science/CPSC_203/CPSC_203_Template/Lecture_Template/Lecture_19)
The functional style of programming is very similar to the idea we learned in databases of building an analysis up out of sequential queries, where the output of one query is input to the next. In this case, you begin with building simple functions; and then more complex functions that call those simple functions.
The basics of the Functional Style of Programming could be summarized as follows:
- A function should do ONE THING ONLY. The one thing it does is Return a Value. That Value can then be used as input to another function.
- Identify the simplest functions you can build.
- Build these functions first.
- Build more complex functions out of the simpler functions.
- If a function appears to be doing more than one thing only, break it down into 2 (or more) functions.
- If you can't build the function you want out of existing functions -- identify the next function you need to build.
- If a function looks to be getting quite long -- think whether you could break it down into simpler functions.
- If the same pattern of code shows up in several functions -- can you put this pattern into it's own function.
The result of this style of programming is that:
- Functions are re-usable in several programs
- You can effectively treat a well detailed and error-checked function as a black box, or "lego" piece that can be used to construct larger functions.
- Large programs, are essentially constructed out of many small functions --each of which is relatively easy to understand.
- You usually need to debug within a particular function --- and not everywhere through a large program.
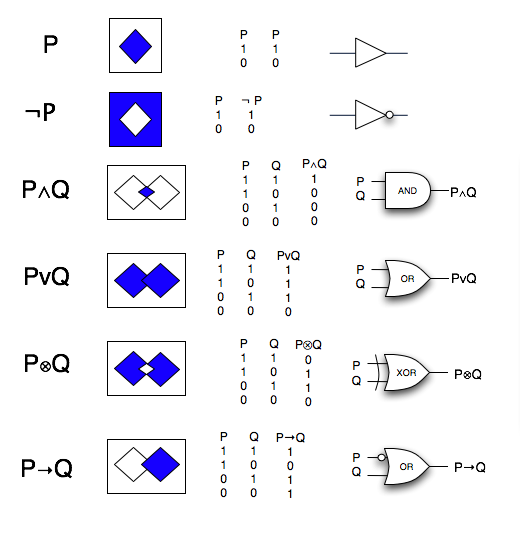
Brief Review of Boolean Logic
This is a summary of the basic Boolean Logic operators we have covered so far, from three different view points:
- Set Theoretic Interpretation
- Truth Table Representation
- Circuit Diagram Visualization of a Truth Table.
3 Views : Set Theory, Truth Tables & Circuits
Note: for P--> Q, the rectangle that surrounds the squares should be fully shaded.
Code Examples of Boolean Logic Functions
Below are examples of the simple Boolean Functions we built in class today, with some error simple error checking code added. Note: the lines in bold are actually marked by triple quotation marks before and after (a form of commenting in Python).
Boolean Functions
def booleanIdentity(x1):
booleanIdentity Rule: Return x1
# Check that input is a boolean value
checkBooleanInputs(x1,0)
return x1
def booleanNot(x1):
booleanNot Rule: Return the absolute value of 1 -x1
# Check input is a boolean value
checkBooleanInputs(x1,0)
return abs(1-x1)
def booleanAnd(x1,x2):
booleanAnd Rule: An AND function takes the minimum of its inputs
# Check the Inputs are Boolean values 0/1
checkBooleanInputs(x1,x2)
# Apply AND Rule
return min(x1,x2)
def booleanOr(x1, x2):
booleanOr Rule: An OR function takes the maximum of its inputs
#Check the Inputs are Boolean values 0/1
checkBooleanInputs(x1,x2)
#Apply OR Rule
return max(x1,x2)
def booleanXor(x1,x2):
boolean Xor Rule: If AND=1, Return 0; else Return OR
#Check the Inputs are Boolean values 0/1
checkBooleanInputs(x1,x2)
# AND=1, returns 0
if booleanAnd(x1,x2) ==1:
return 0
# else return OR
else:
return booleanOr(x1,x2)
def booleanImplication(x1,x2):
booleanImplication Rule: Not-X or Y
# Check Inputs are Boolean values 0/1
checkBooleanInputs(x1,x2)
# Not X
notX = booleanNot(x1)
# Or Y
boolImp = booleanOr(notX,x2)
return boolImp
class BooleanError(Exception):
def __init__(self, msg, x1, x2):
self.arg = (msg, x1, x2)
self.msg = msg
self.x1 = x1
self.x2 =x2
def __str__(self):
return str(self.arg)
def checkBooleanInputs(x1,x2):
Raises an Error Message if Inputs are not 1 or 0
if (x1 not in [1,0]) or (x2 not in [1,0]):
raise BooleanError ("NonBoolean Inputs", x1, x2)